what is the area of a circle with a radius of 15 inches to the nearest tenth use 3.14 for pi
Expanse and circumference of circle estimator uses radius length of a circumvolve, and calculates the perimeter and surface area of the circle. Information technology is an online Geometry tool requires radius length of a circle. Using this figurer, we will sympathise methods of how to find the perimeter and surface area of a circumvolve.
Information technology is necessary to follow the next steps:
- Enter the radius length of a circle in the box. The value must be positive existent number or parameter. Annotation that the length of a segment is always positive;
- Press the "GENERATE Piece of work" push to make the computation;
- Circle estimator will give the perimeter and area of a circle.
Input : A positive real number or parameter as the radius length of a circle;
Output : Two positive real numbers or variables as the perimeter and area of a circle and corresponding units after that.
Circle Formula :
Circumference (Perimeter) of Circle Formula: The circumference of a circle is adamant by the following formula $$C=D\times\pi$$ where $D$ is the length of the bore of the circle and $\pi\approx3.14$.
Circumference (Perimeter) of Circle Formula: The circumference of a circle is adamant by the post-obit formula $$C=2\times r\times\pi$$ where $r$ is the length of the radius of the circle and $\pi\approx3.14$.
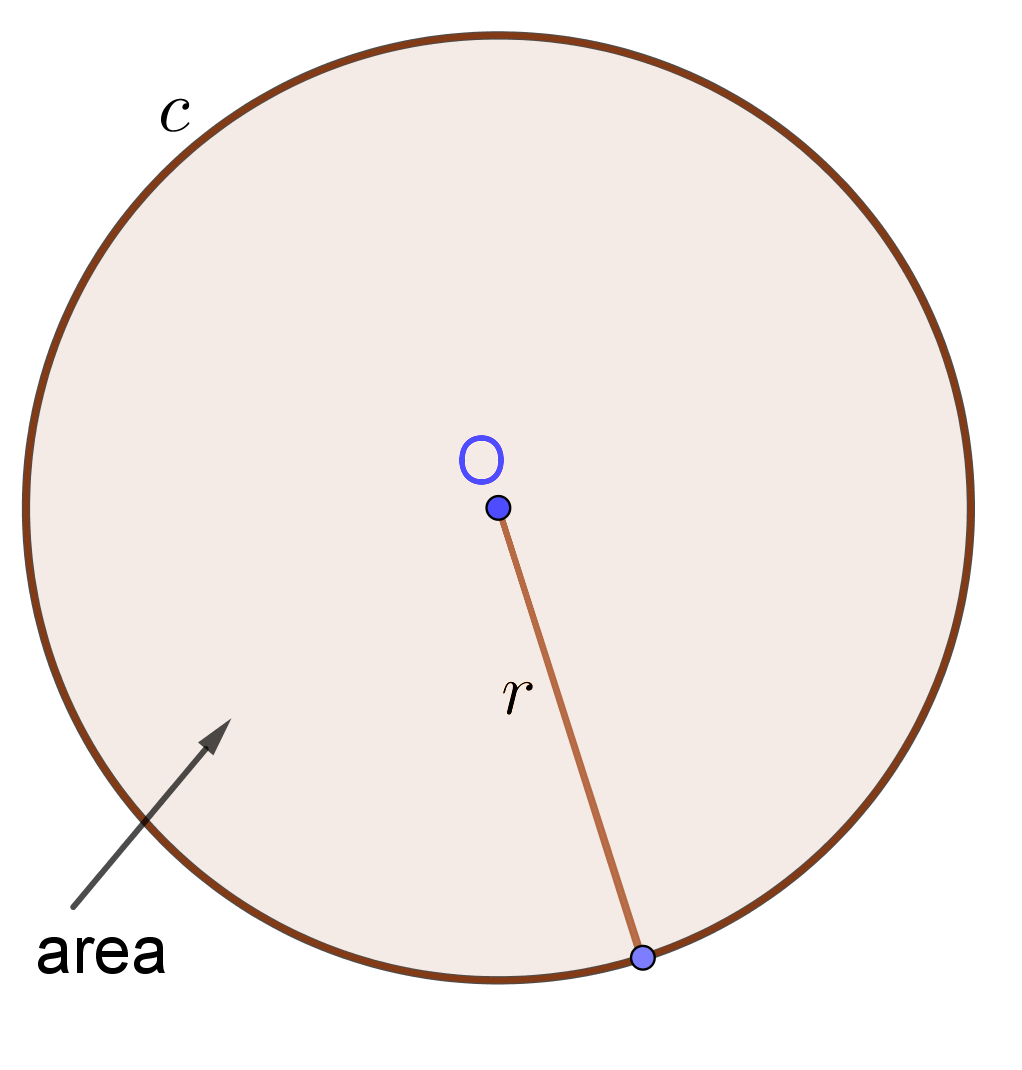
Area of Circle Formula: The area of a circumvolve is adamant past the following formula $$A=r\times r\times\pi=r^2\times \pi$$ where $r$ is the length of the radius of the circle and $\pi\approx3.14$.
What is Area & Perimeter of Circle?
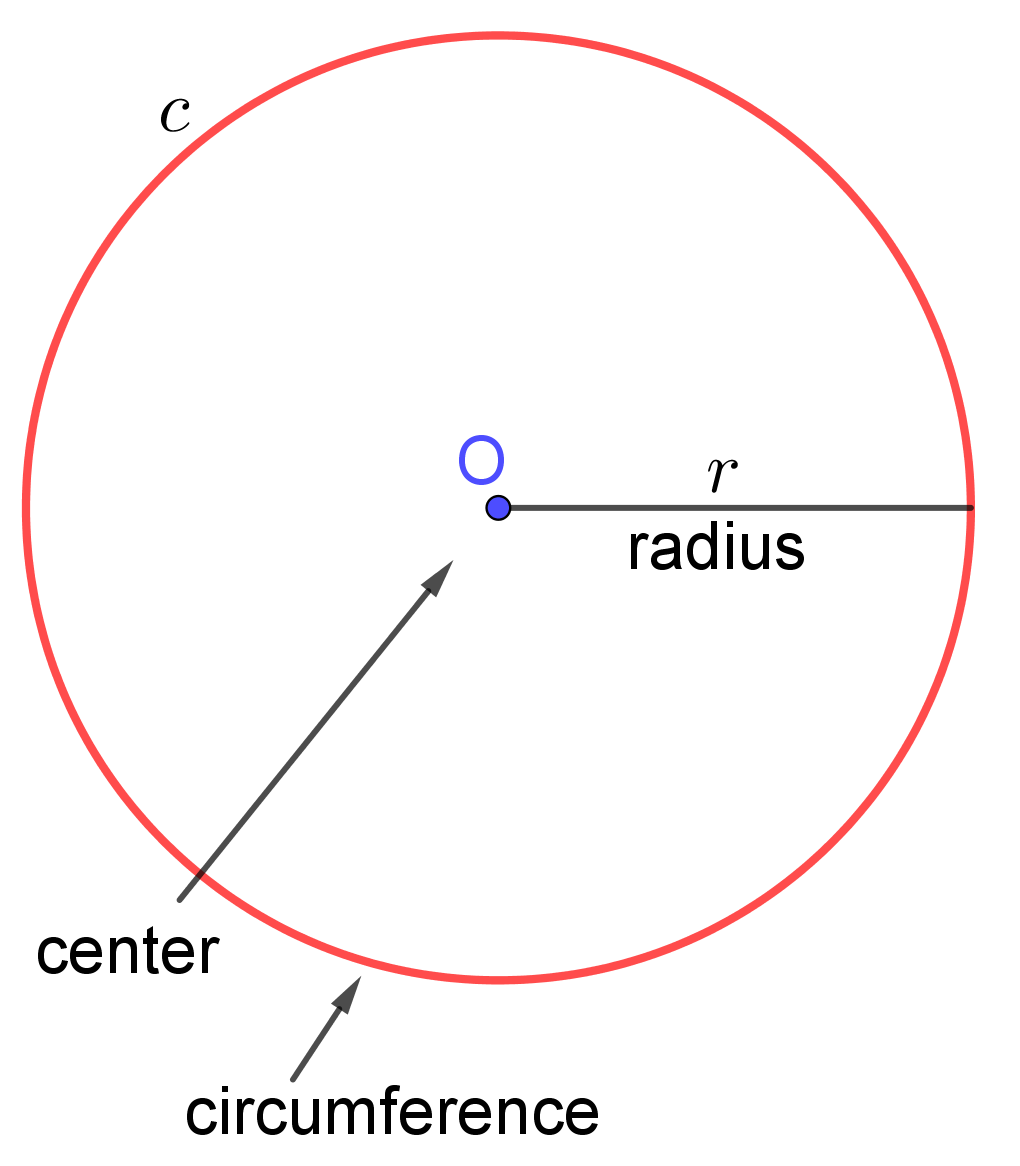
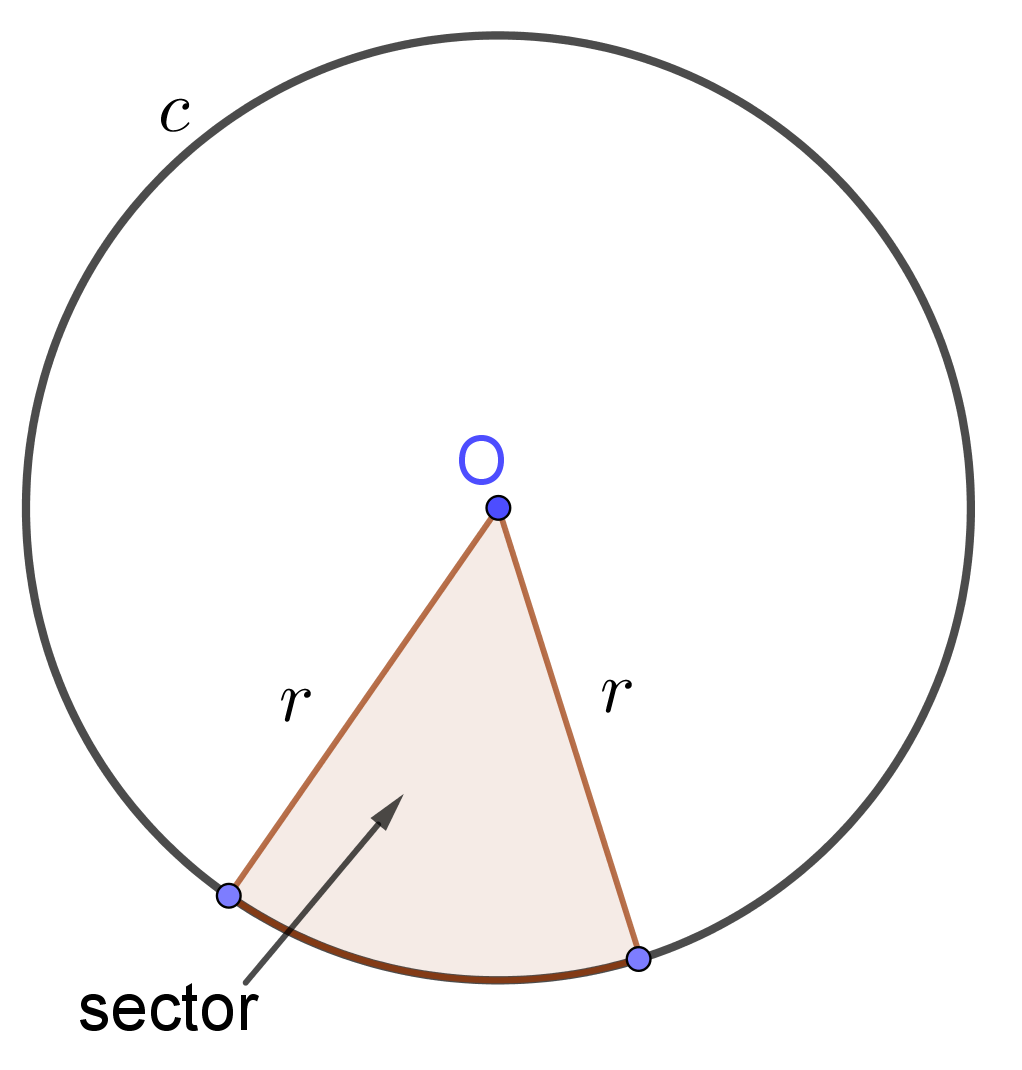
A gear up of points in a plane equally distanced from a given indicate $O$ is a circumvolve. The betoken $O$ is chosen the center of the circle. The distance from the center of a circumvolve to any signal on the circumvolve is chosen the radius of this circumvolve.A radius of a circle must be a positive real number. The circle with a center $O$ and a radius $r$ is denoted by $c(O,r)$.
The distance around a circle is called the perimeter or circumference of the circumvolve. It is unremarkably denoted by $C$.

If all vertices of a polygon belong on a circle, then the polygon is called inscribed. If all sides of a polygon are tangent to a circle, then the polygon is chosen circumscribed.
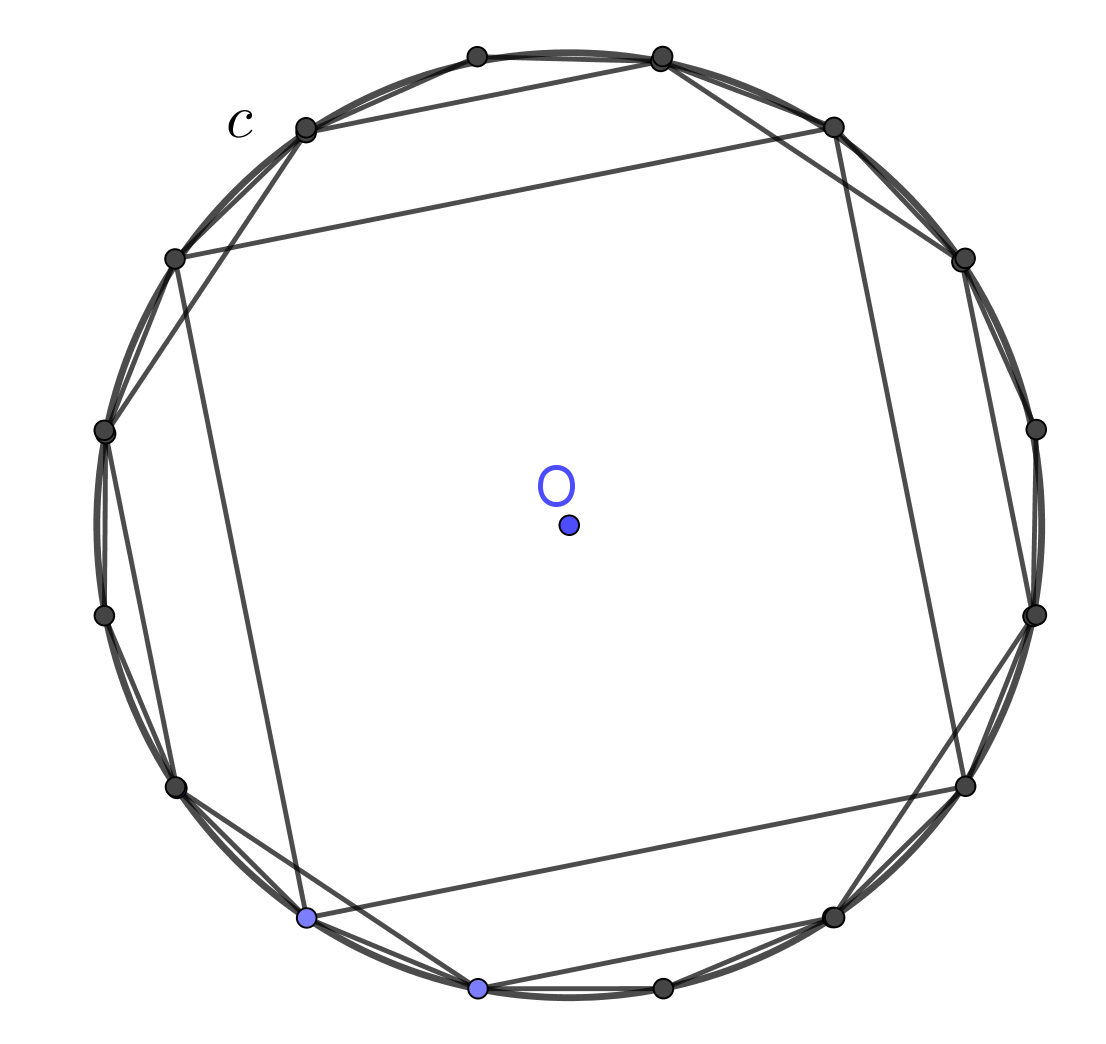
Method for finding circumference of circle: Allow us inscribe into a circle a regular polygon, for example square. Then double the number of sides of this polygon to get octagon. If we continue the process of doubling the number of sides of regular inscribed polygons, we obtain an infinite sequence of perimeters of regular polygons which increases. This increasing sequence is divisional, since perimeters of all inscribed convex polygons are less than the perimeter of any circumscribed polygon. And then, this increasing sequence of perimeters has a certain limit. This limit is the circumference. Hence, the circumference of a circle is the limit of the perimeter of a regular polygon inscribed into the circle when the number of its vertices is doubled indefinitely. Because all circles are similar, the ratio of the circumference to the diameter is the same number for all circles. This ratio of circumference to diameter is denoted by the Greek letter $\pi\approx three.fourteen$. Thus, the formula for circumference is
$$C=D\times \pi$$
or
$$C=2\times r\times \pi$$
Archimedes [Heath, T. L., it A History of Greek Mathematics, 2 vol., Oxford, 1921] gave approximation of $\pi$, by $$\pi\approx \frac{22}7= iii.142857142857...$$
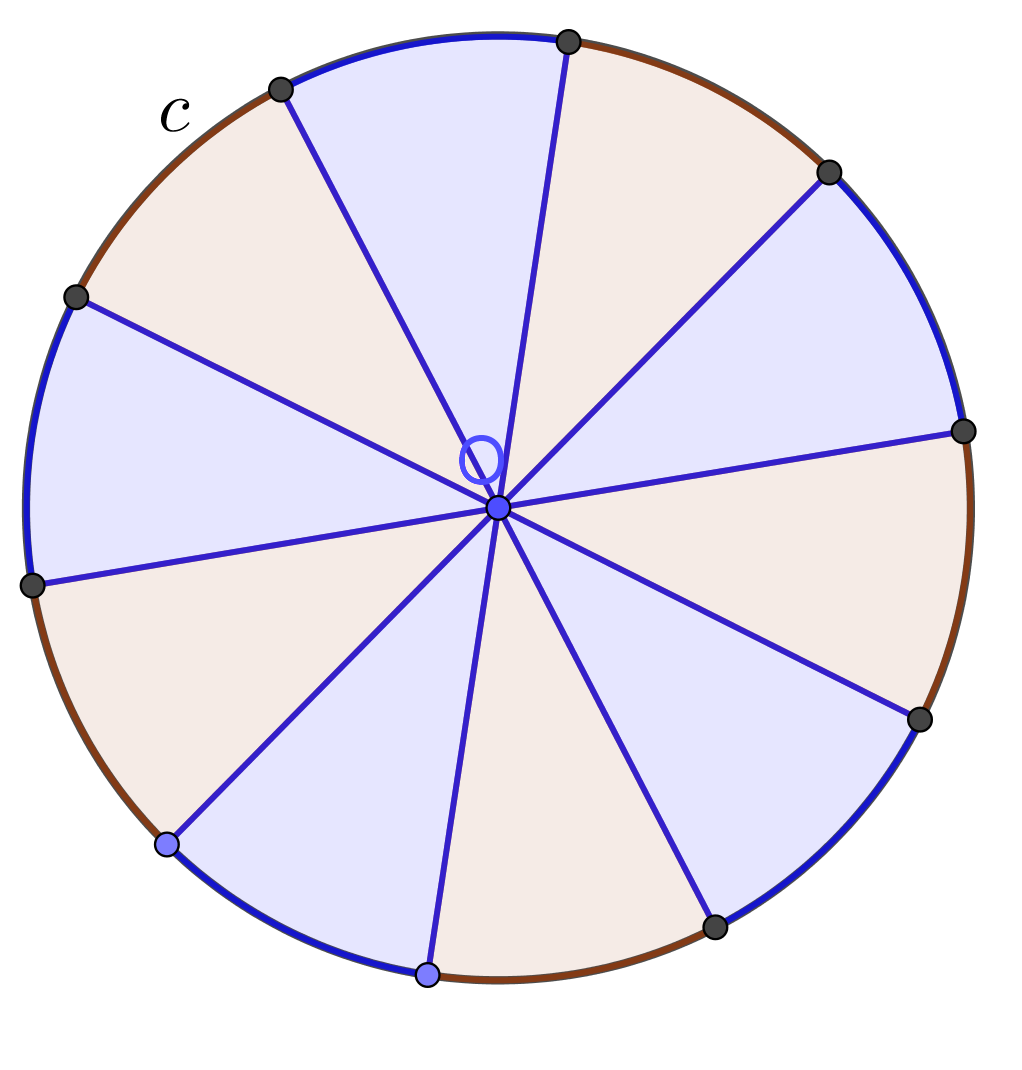
Method for finding expanse of circle: The area of a circle is the number of foursquare units within that circle. By dividing a circle into equal parts as shown in the picture below, we can rearrange the parts into an gauge rectangle. The length of this approximate rectangle equals the half of the circumference of the circumvolve, $r\times\pi$. The width of this approximate rectangle is the radius $r$ of the circle. Since the area of a rectangle is the production of its length and width, the area of this gauge rectangle is
$$A=r\times r\times \pi=r^2\times\pi$$
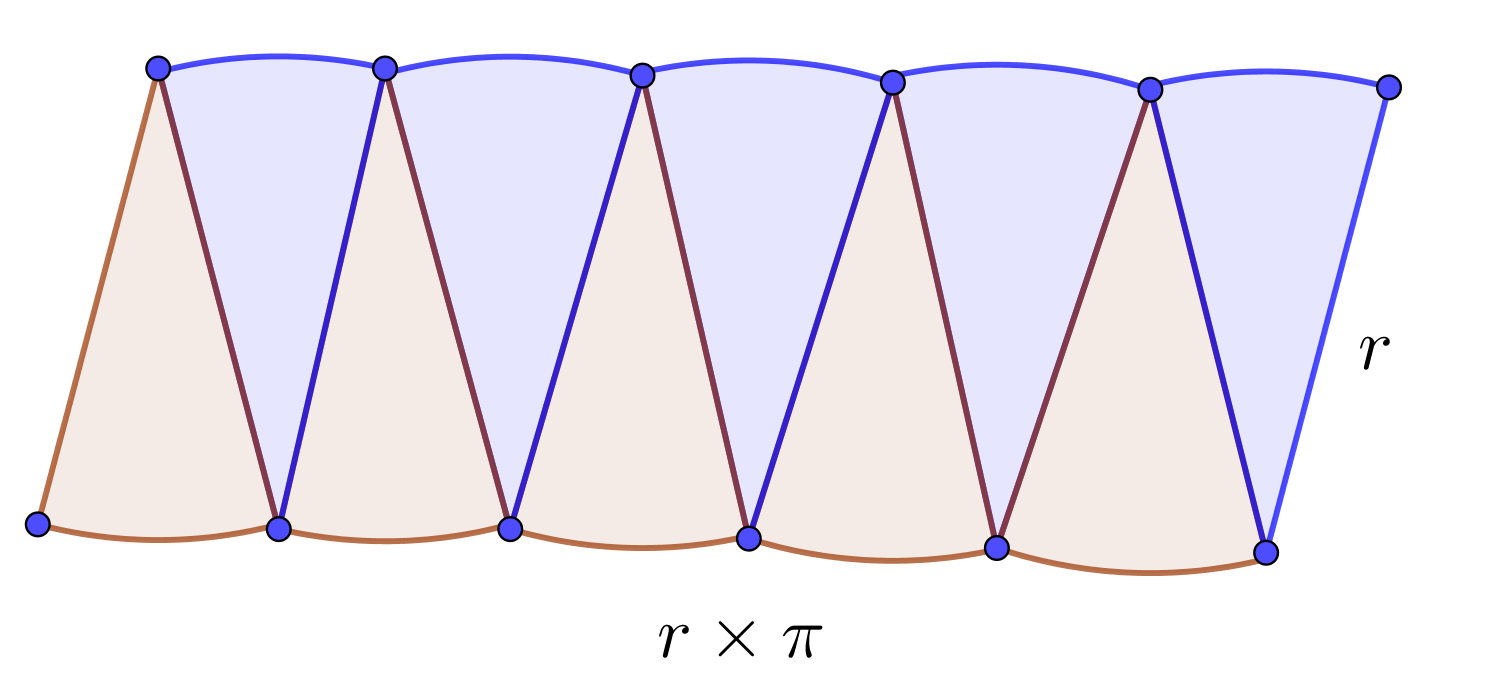
The perimeter is measured in units such as centimeters,meters, kilometers, inches, anxiety, yards, and miles. The expanse is measured in units such equally square centimeters $(cm^ii)$, square meters $(1000^2)$, square kilometers $(km^2)$ etc.
The Area and perimeter of a circle piece of work with steps shows the complete stride-by-step calculation for finding the circumference and expanse of the circle with the radius length of $8\;in$ using the circumference and area formulas. For whatsoever other value for the length of the radius of a circle, just supply a positive real number and click on the GENERATE Work button. The grade schoolhouse students may use this circle calculator to generate the work, verify the results of perimeter and area of ii dimensional figures or do their homework problems efficiently. They can apply these methods in order to decide the area and lengths of parts of a circumvolve.
Real World Problems Using Area and Perimeter of a Circle
Calculating areas and circumferences of circles plays an of import function in almost all field of science and real life. For instance, formula for circumference and surface area of a circle can be applied into geometry. They are used to explore many other formulas and mathematical equations. An arch length is a portion of the circumference of a circle. The ratio of the length of an arc to the circumference is equal to the ratio of the mensurate of the arc to $360$ degrees. A sector of a circles is the region divisional by 2 radii of the circle and their intercepted arc.
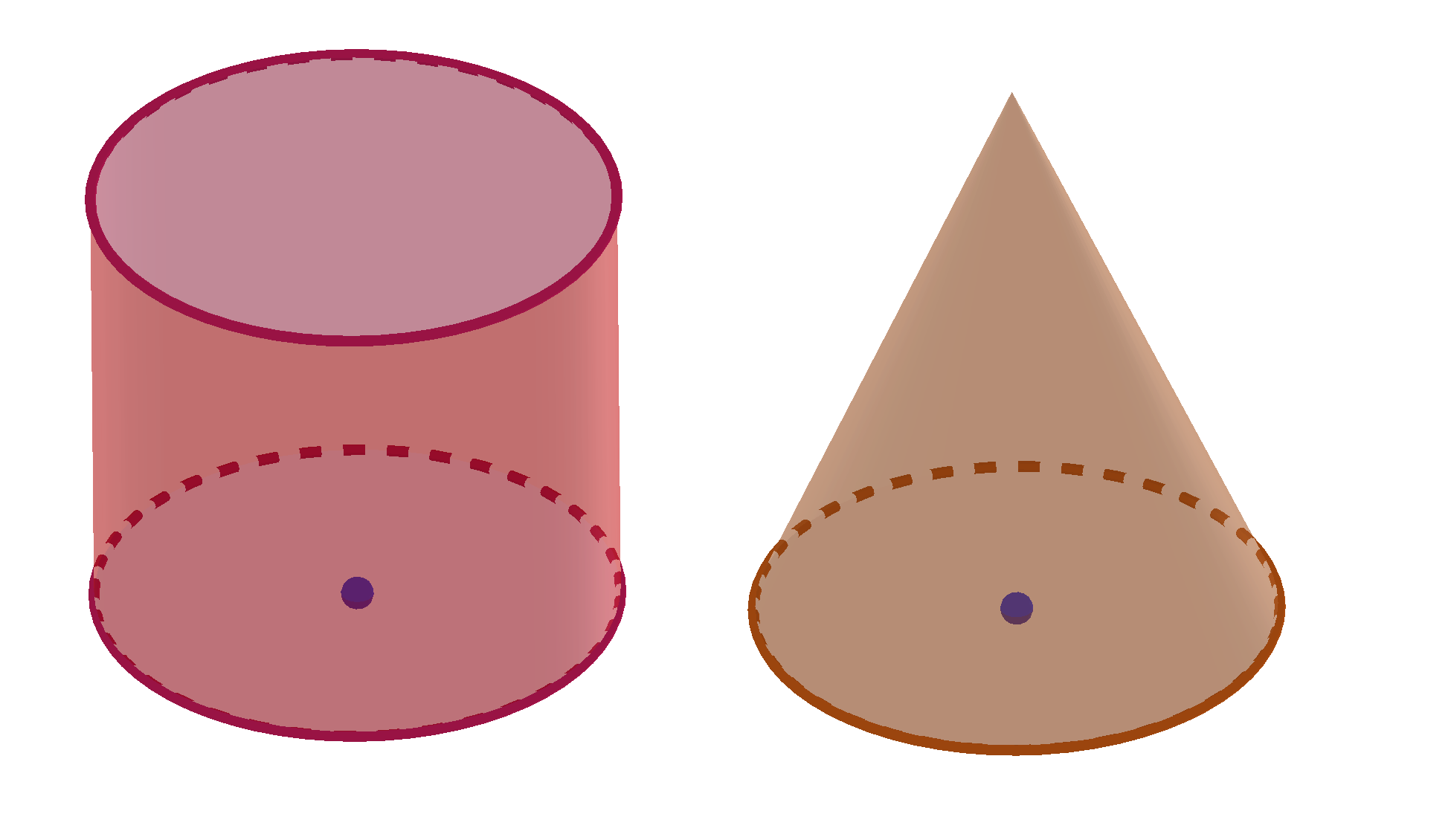
The area and volume of a cylinder and cone with circular bases contain the formula for area of circle. The lateral surface of a cone consists of all segments that connect the vertex with points on the base. If we cut information technology along the slant height then the lateral surface is the sector of a circle. So, the lateral expanse of a cone as well uses the formula for area of circle.
Circle Practice Problems
Practise Problem 1:
A pizza is divided into $eight$ equal pieces. The diameter of the pizza is $25$ centimeters. Find the surface area of 1 piece of pizza.
Practice Problem ii:
Given a tire with diameter of $100$ centimeters. How many revolutions does tire make while traveling $10$ kilometers?
The circle reckoner, formula, example calculation (work with steps), real globe bug and exercise issues would be very useful for grade school students (Grand-12 education) to sympathise the concept of perimeter and area of circle. This concept can be of significance in geometry, to find the perimeter, area and volume of solids. Real life problems on circles involving arc length, sector of a circumvolve, expanse and circumference are very common, so this concept can be of dandy importance of solving problems.
morrisonnetionster.blogspot.com
Source: https://ncalculators.com/geometry/circle-calculator.htm
0 Response to "what is the area of a circle with a radius of 15 inches to the nearest tenth use 3.14 for pi"
Post a Comment